[1] Linked List 의 개념과 java Collection 살펴보기
Linked List란?
일련의 Node(여기서 Node란, Data와 Pointer를 가지고 있는 기본 단위)들이 다음 노드(또는 이전 노드)를 가리키는 방식으로 서로를 참조하는 선형 자료구조.
특징
실제로 메모리가 연속하는 건 아님(배열과의 차이). (배열은 처음부터 정적으로 메모리 크기를 할당하고, 그 속에서 해당 자료형의 크기 * N으로 N번째 메모리에 한 번에 접근 가능함) -> 메모리가 각각 독립적인 공간에 존재하고, pointer로 위치를 참조함.
동적인 크기를 가짐. 노드의 추가 삭제로, 해당 자료구조의 크기가 동적으로 변함.

시간 복잡도에서의 Linked List
데이터의 조회, 추가, 삭제, 수정을 기준
1. 조회
Linked List의 데이터들은 특정 순서를 가지지 않기 때문에, 특정 데이터를 찾기 위해서는 N개의 데이터를 모두 탐색할 수밖에 없습니다. Java의 Collection의 contains 메서드를 보면 다음과 같습니다.
public int indexOf(Object o) {
int index = 0;
if (o == null) {
for (Node<E> x = first; x != null; x = x.next) {
if (x.item == null)
return index;
index++;
}
} else {
for (Node<E> x = first; x != null; x = x.next) {
if (o.equals(x.item))
return index;
index++;
}
}
return -1;
}해당 object를 찾을 때까지 first 노드부터 순차적으로 탐색하는 모습입니다. 따라서 시간복잡도는 O(N)이겠네요!
2. 추가
추가는 여러 상황이 있습니다. Linked List의 특징에 맞게, 중간 지점에서 두 노드의 연결을 끊고, 새로운 노드를 추가할 수도 있습니다. 또는 처음과 끝에 노드를 연결할 수도 있어요. 각 상황에 따라 시간복잡도가 다르게 나옵니다.
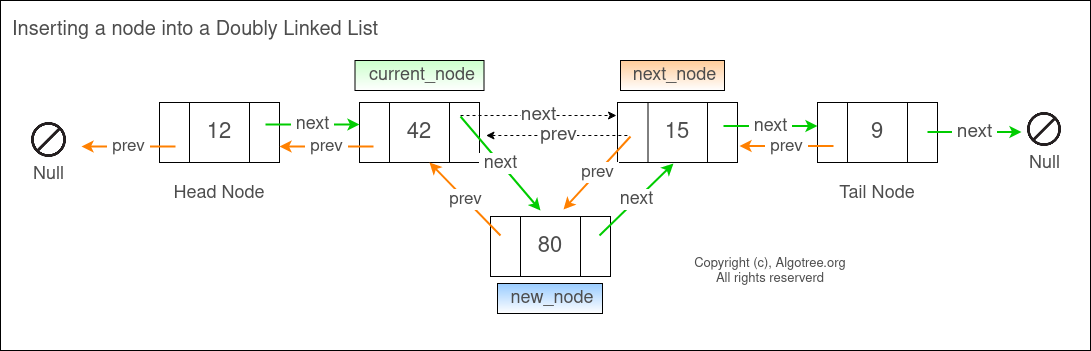
처음이나 마지막에 노드를 추가할 때는, 단순히 head 또는 tail과 첫 번째 또는 마지막 노드 사이에 하나의 노드를 추가하면 되기 때문에, 시간복잡도는 O(1)로 예상됩니다.
하지만 중간 지점에 노드를 추가하려 할 때는, 최대 (N/2)번 노드를 탐색하고, 해당 Node에서 추가되므로 시간복잡도는 O(N)으로 예상됩니다. Java Collections의 코드를 살펴볼게요.
우선 addFirst method입니다. first 노드(prev 주솟값은 null이고 next 주솟값은 가지고 있는 시작 node)를 새로 넣어주는 node로 교체해주는 방식으로 진행됩니다. 한 번의 메서드 수행으로 추가가 완료되므로 시간복잡도는 O(1)입니다.
private void linkFirst(E e) {
final Node<E> f = first;
final Node<E> newNode = new Node<>(null, e, f);
first = newNode;
if (f == null)
last = newNode;
else
f.prev = newNode;
size++;
modCount++;
}addLast도 동일한 방식입니다. Last를 교체하는 방식으로 진행됩니다.
이제 add(index, element) method를 살펴볼게요.
public void add(int index, E element) {
checkPositionIndex(index);
if (index == size)
linkLast(element);
else
linkBefore(element, node(index));
}
Node<E> node(int index) {
// assert isElementIndex(index);
if (index < (size >> 1)) {
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}checkPositionIndex는 index의 유효성을 검사하는 method입니다. index와 size의 비교를 한 번 수행합니다.
node(index)는 index 번째 node를 찾는 method입니다. size/2를 기준으로 앞에서부터 탐색할지, 뒤에서부터 탐색할지 나눠두었네요. 여기서 시간복잡도가 결정이 됩니다. 해당 node를 찾아가기 위해 최대 (N/2)번의 반복문이 수행되므로, 삽입할 node를 찾아가기 위한 시간복잡도는 O(N)입니다.
index와 size가 같으면 위에서 수행해본 addLast로 1회의 수행으로 끝낼 수 있고, linkBefore 메서드는 다음과 같아요.
void linkBefore(E e, Node<E> succ) {
// assert succ != null;
final Node<E> pred = succ.prev;
final Node<E> newNode = new Node<>(pred, e, succ);
succ.prev = newNode;
if (pred == null)
first = newNode;
else
pred.next = newNode;
size++;
modCount++;
}index 번째 node를 succ라 하고, succ의 이전 노드를 pred라 했을 때, pred와 succ 사이에 새로운 node를 추가하는 방식으로 진행됩니다. 그러면 정확하게 index 번째에 새로운 노드를 넣을 수 있겠네요. 그러면 여기서 반복문이나, method가 여러 번 실행되는 모습은 보이지 않는데요. 실제로 해당 node를 찾은 후에는 포인터만 변경해 주면 되므로 시간복잡도는 O(1)입니다.
최종 시간복잡도: O(N) + O(1) => O(N)
3. 삭제
특정 node를 삭제하는 방식에도 여러 가지가 있어요.
단순히 첫 번째, 또는 마지막 노드를 삭제할 수도 있을 것이고, 또는 특정 인덱스를 삭제할 수도 있을 것입니다.
특정 값을 가진 node를 삭제할 수도 있겠죠(중복된 node들이 있다면 모든 node를 삭제시킬 수도, 그중 첫 번째를 삭제시킬 수도 있습니다.)
자바에서의 삭제는 해당 노드와의 연결을 끊는 식으로 진행됩니다. 저희의 프로그램이 특정 주솟값에 대한 접근 방법을 잃으면 GC가 해당 메모리를 알아서 초기화해 줍니다.
추가와 마찬가지로 첫 노드와 마지막 노드의 시간복잡도는 O(1), 특정 node를 삭제하거나 특정 index 노드를 삭제하려면 모든 데이터의 조회 과정이 필요하므로 시간복잡도 O(N)이 예상됩니다.
Collections 코드를 통해 시간복잡도를 확인해 보겠습니다.
첫 번째 노드를 제거하는 method입니다. first 노드를 f로 입력받고, f.next를 null로 설정해 접근 방법을 없애 gc가 알아서 처리해 주도록 하는 방식입니다. 반복되는 메서드는 없이 한 번의 수행으로 삭제 가능하므로 시간복잡도는 O(1)입니다.
private E unlinkFirst(Node<E> f) {
// assert f == first && f != null;
final E element = f.item;
final Node<E> next = f.next;
f.item = null;
f.next = null; // help GC
first = next;
if (next == null)
last = null;
else
next.prev = null;
size--;
modCount++;
return element;
}특정 index의 노드를 제거하는 코드입니다. 마찬가지로 index 번째 node를 찾는 데 O(N)의 시간복잡도가 필요하고, 해당 node를 찾은 후, 해당 node의 prev와 next를 연결해주는 방식입니다.
public E remove(int index) {
checkElementIndex(index);
return unlink(node(index));
}
E unlink(Node<E> x) {
// assert x != null;
final E element = x.item;
final Node<E> next = x.next;
final Node<E> prev = x.prev;
if (prev == null) {
first = next;
} else {
prev.next = next;
x.prev = null;
}
if (next == null) {
last = prev;
} else {
next.prev = prev;
x.next = null;
}
x.item = null;
size--;
modCount++;
return element;
}특정 값을 가진 node를 제거하는 method입니다. 마찬가지로 unlink 메서드가 사용되고, Collections에서는 first부터 탐색하기 시작하여 특정 값을 가진 node가 나타나면 제거하고 method가 종료되므로, 중복된 값을 가지고 있는 Linked List의 경우 첫 번째 값을 가진 node가 제거됩니다. 시간복잡도는 첫 번째 node부터 해당 값을 가지고 있는 node까지 탐색하므로 최대 n번의 수행이 필요하므로 O(N)입니다.
public boolean remove(Object o) {
if (o == null) {
for (Node<E> x = first; x != null; x = x.next) {
if (x.item == null) {
unlink(x);
return true;
}
}
} else {
for (Node<E> x = first; x != null; x = x.next) {
if (o.equals(x.item)) {
unlink(x);
return true;
}
}
}
return false;
}4. 수정
특정 index 노드를 찾고, 해당 node의 데이터를 변경하는 순서로 진행됩니다. Collection의 메서드는 다음과 같습니다.
public E set(int index, E element) {
checkElementIndex(index);
Node<E> x = node(index);
E oldVal = x.item;
x.item = element;
return oldVal;
}마찬가지로, node(index)에서 O(N)의 시간복잡도가 필요하고, 데이터의 변경에는 O(1)의 시간복잡도가 소모됩니다.
따라서 수정에 필요한 시간복잡도는 O(N)입니다.
